【理論】令和28年 問9|RLC直並列回路における共振周波数の計算問題
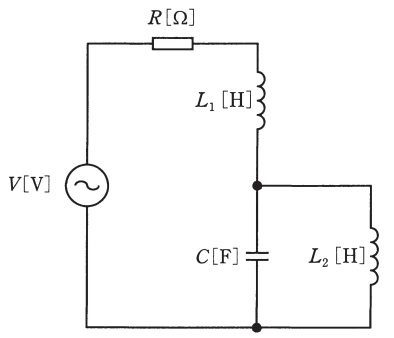
図のように,\( R = 1 \) [Ω] の抵抗,インダクタンス \( L_1 = 0.4 \) [mH],\( L_2 = 0.2 \) [mH] のコイル,及び静電容量 \( C = 8 \) [μF] のコンデンサからなる直並列回路がある。
この回路に交流電圧 \( V = 100 \) [V] を加えたとき,回路のインピーダンスが極めて小さくなる直列共振周波数 \( \omega_1 \) の値 [rad/s] 及び回路のインピーダンスが極めて大きくなる並列共振周波数 \( \omega_2 \) の値 [rad/s] の組合せとして,最も近いものを次の (1)~(5) のうちから一つ選べ。
| ω1 | ω2 | |
|---|---|---|
| (1) | 2.5 × 104 | 3.5 × 103 |
| (2) | 2.5 × 104 | 3.1 × 104 |
| (3) | 3.5 × 103 | 2.5 × 104 |
| (4) | 3.1 × 104 | 3.5 × 103 |
| (5) | 3.1 × 104 | 2.5 × 104 |
合格への方程式
RLC回路の基本原理
RLC回路とは、抵抗(Resistance)、インダクタ(Inductance)、コンデンサ(Capacitance)を組み合わせた回路です。これらの素子は交流回路において、それぞれ異なる性質を示します。
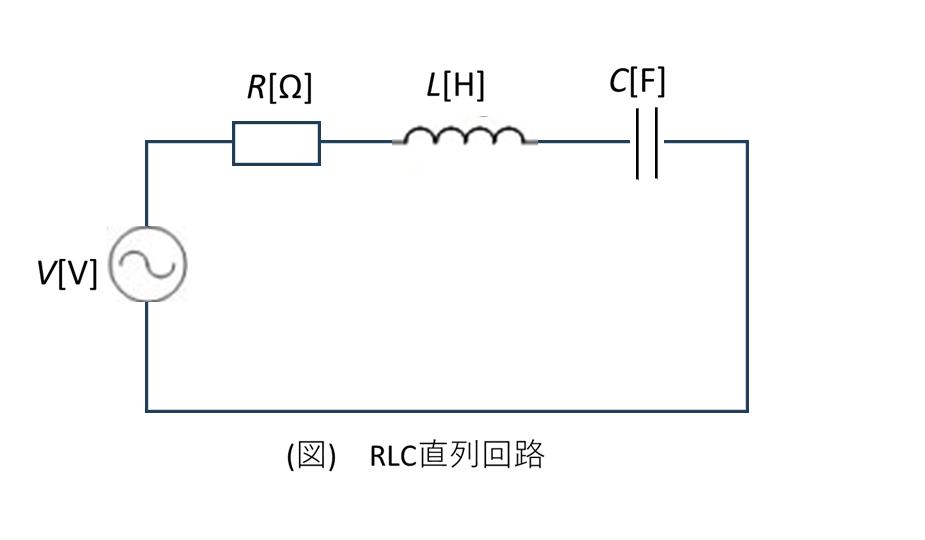
図1: RLC直列回路
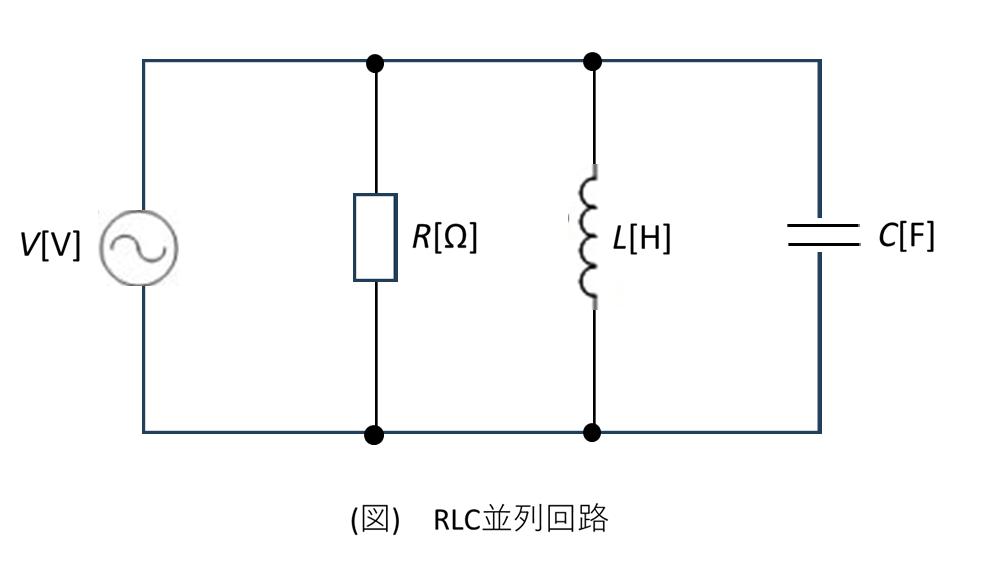
図2: RLC並列回路
各素子の基本特性
| 素子 | 記号 | インピーダンス | 位相特性 |
|---|---|---|---|
| 抵抗 | R | \(R\) [\(\Omega\)] | 電圧と電流が同相 |
| インダクタ | L | \(j\omega L\) [\(\Omega\)] | 電圧が電流より90°進む(電流が電圧より90°遅れる) |
| コンデンサ | C | \(\frac{1}{j\omega C}\) [\(\Omega\)] | 電圧が電流より90°遅れる(電流が電圧より90°進む) |
重要なポイント
RLC回路では、インダクタとコンデンサの特性が周波数に依存します。これにより、特定の周波数(共振周波数)において回路の特性が大きく変化します。
直列RLC回路のインピーダンス
直列接続された場合、合成インピーダンス \(\dot{Z}\) は各素子のインピーダンスの和になります:
\[ \begin{aligned} \dot{Z} &= R + j\omega L + \frac{1}{j\omega C} \\[10pt] &= R + j\left(\omega L - \frac{1}{\omega C}\right) \end{aligned} \]
並列RLC回路のアドミタンス
並列接続された場合、合成アドミタンス \(\dot{Y}\)(インピーダンスの逆数)は各素子のアドミタンスの和になります:
\[ \begin{aligned} \dot{Y} &= \frac{1}{R} + j\omega C + \frac{1}{j\omega L} \\[10pt] &= \frac{1}{R} + j\left(\omega C - \frac{1}{\omega L}\right) \end{aligned} \]
補足説明
インピーダンス \(\dot{Z}\) とアドミタンス \(\dot{Y}\) は互いに逆数の関係にあります:\(\dot{Y} = \frac{1}{\dot{Z}}\)。直列回路ではインピーダンスで、並列回路ではアドミタンスで考えると計算が簡単になります。
共振条件と特性
RLC回路において「共振」とは、回路のリアクタンス成分(インダクタンスとキャパシタンス)が打ち消し合い、特殊な状態になる現象です。これは水面の波や振り子の共振と似た物理現象です。
直列共振回路の条件
直列RLC回路では、インピーダンスが最小になる条件が共振状態です。
\[ \begin{aligned} \omega_c L - \frac{1}{\omega_c C} &= 0 \\[10pt] \omega_c L &= \frac{1}{\omega_c C} \\[10pt] \omega_c^2 &= \frac{1}{LC} \\[10pt] \omega_c &= \frac{1}{\sqrt{LC}} \end{aligned} \]
共振時の特性(直列回路)
- インピーダンスは純抵抗 \(Z = R\) になる
- 電流が最大になる
- 電圧と電流が同相になる
- 力率が1になる
並列共振回路の条件
並列RLC回路では、アドミタンスが最小(インピーダンスが最大)になる条件が共振状態です。
\[ \begin{aligned} \omega_c C - \frac{1}{\omega_c L} &= 0 \\[10pt] \omega_c C &= \frac{1}{\omega_c L} \\[10pt] \omega_c^2 &= \frac{1}{LC} \\[10pt] \omega_c &= \frac{1}{\sqrt{LC}} \end{aligned} \]
共振時の特性(並列回路)
- インピーダンスは純抵抗の逆数 \(Y = \frac{1}{R}\) になる
- 電流が最小になる
- 電圧と電流が同相になる
- 力率が1になる
注意点
直列共振と並列共振は、同じ共振角周波数 \(\omega_c = \frac{1}{\sqrt{LC}}\) を持ちますが、回路の振る舞いは異なります。直列共振では電流が最大になる一方、並列共振では電流が最小になります。
共振周波数とQ値
共振回路の鋭さを表す指標として「Q値」(品質係数)があります。Q値が高いほど、共振のピークが鋭くなります。
直列共振回路のQ値:
\[ Q = \frac{\omega_c L}{R} = \frac{1}{\omega_c CR} \]
並列共振回路のQ値:
\[ Q = R\sqrt{\frac{C}{L}} = \omega_c CR \]
Q値の物理的意味
Q値は、共振回路に蓄えられるエネルギーと1周期あたりに消費されるエネルギーの比率を表します。高いQ値は、エネルギー損失が少なく、共振が持続しやすいことを意味します。
計算例と応用
共振周波数の計算例
例題1
インダクタンス \(L = 10\) [mH]、キャパシタンス \(C = 1\) [μF] のRLC直列回路の共振周波数を求めなさい。
解答
\[ \begin{aligned} \omega_c &= \frac{1}{\sqrt{LC}} \\[10pt] &= \frac{1}{\sqrt{10 \times 10^{-3} \times 1 \times 10^{-6}}} \\[10pt] &= \frac{1}{\sqrt{10 \times 10^{-9}}} \\[10pt] &= \frac{1}{10^{-4} \times \sqrt{10}} \\[10pt] &\approx 3162 \text{ [rad/s]} \end{aligned} \]
周波数に変換すると:
\[ \begin{aligned} f_c &= \frac{\omega_c}{2\pi} \\[10pt] &\approx \frac{3162}{2\pi} \\[10pt] &\approx 503 \text{ [Hz]} \end{aligned} \]
例題2
共振周波数 \(f_c = 1\) [kHz] のRLC並列回路を設計したい。\(L = 50\) [mH] とすると、必要なコンデンサの容量 \(C\) はいくらか。
解答
\[ \begin{aligned} \omega_c &= 2\pi f_c = 2\pi \times 1000 = 6283 \text{ [rad/s]} \\[10pt] \omega_c &= \frac{1}{\sqrt{LC}} \\[10pt] \therefore C &= \frac{1}{\omega_c^2 L} \\[10pt] &= \frac{1}{6283^2 \times 50 \times 10^{-3}} \\[10pt] &\approx 0.5 \times 10^{-6} \text{ [F]} \\[10pt] &= 0.5 \text{ [μF]} \end{aligned} \]
RLC回路の主な応用
| 応用分野 | 使用する回路 | 目的・特徴 |
|---|---|---|
| ラジオ受信機 | 並列共振回路 | 特定の周波数の電波だけを選択的に受信 |
| 同調フィルタ | 直列/並列共振回路 | 特定の周波数帯域を通過/阻止 |
| 電力系統の力率改善 | 並列RLC回路 | 無効電力の補償による力率向上 |
| 発振回路 | RLC共振回路 | 特定周波数の信号発生 |
補足説明
RLC共振回路は日常生活の多くの電子機器に使われています。例えば、スマートフォンのRFIDや非接触充電も共振現象を利用しています。
発展と関連回路
バンドパスフィルタとしてのRLC回路
RLC共振回路は特定の周波数帯域を通過させるバンドパスフィルタとして機能します。
バンドパスフィルタの特性
- 中心周波数:\(f_c = \frac{1}{2\pi\sqrt{LC}}\)
- 帯域幅:\(\Delta f = \frac{R}{2\pi L}\)(直列共振回路の場合)
- 選択度:\(Q = \frac{f_c}{\Delta f}\)
複合共振回路
複数のRLC回路を組み合わせることで、より複雑なフィルタ特性を実現できます。
複合共振回路の例
- 二重同調回路:二つの共振回路を結合させた回路
- バンドストップフィルタ:特定の周波数帯域を阻止する回路
- ハイパスフィルタとローパスフィルタの組み合わせ
非線形RLC回路
実際の回路素子は完全な線形素子ではなく、電圧や電流が大きくなると非線形性が現れます。
非線形効果
- インダクタの鉄心の飽和による非線形性
- コンデンサの誘電体損失と温度依存性
- 抵抗の温度依存性
これらの非線形効果により、理論値と実測値が異なることがあります。
分布定数回路への発展
高周波では、RLC回路は集中定数回路から分布定数回路として扱う必要があります。
分布定数回路の例
同軸ケーブルや伝送線路では、インダクタンスやキャパシタンスが線路に沿って分布しています。このような回路では、波動方程式に基づいた解析が必要になります。
回路シミュレーションによる解析
複雑なRLC回路の解析には、SPICE等のシミュレーションソフトウェアが利用されます。これにより、過渡応答や周波数応答を詳細に調べることができます。
シミュレーションで調べられること
- 共振曲線の形状と帯域幅
- 過渡応答における減衰振動
- パラメータ変化に対する感度分析
🔍 ワンポイントアドバイス: RLC共振回路の計算では、直列と並列で共振周波数は同じですが、インピーダンスの挙動が逆になることを覚えておきましょう。また、Q値は「回路の鋭さ」を表す重要な指標です。試験では、共振条件から未知のパラメータを求める問題がよく出題されます。
今日はRLC回路の共振角周波数について勉強していくで!まずは直列共振のイメージをつかもうか。RC直列回路ではインピーダンスが最小になる周波数があるんやけど、わかるかな?
はい、先生!直列共振では回路のインピーダンスが最小になり、電流が最大になる周波数があります。リアクタンス成分が打ち消しあって、抵抗成分だけが残る状態ですね。
その通りや!じゃあ今回の問題を見てみよか。まずはL₂とCの合成インピーダンスを考えていくで。インピーダンスの合成公式を使うんやけど、覚えてるか?
はい!並列接続の場合、合成インピーダンスは次の式で計算できます:
\( Z_{合成} = \frac{Z_1 \times Z_2}{Z_1 + Z_2} \)
この場合、\(Z_1 = j\omega L_2\)、\(Z_2 = \frac{1}{j\omega C}\) ですね。
その通りや!じゃあ実際に計算してみよか。L₂とCの合成インピーダンスを求めて、それから回路全体のインピーダンスを考えるんや。
わかりました。L₂とCの合成インピーダンスを計算します:
\[ \begin{aligned} Z_{L_2C} &= \frac{j\omega L_2 \cdot \frac{1}{j\omega C}}{j\omega L_2 + \frac{1}{j\omega C}} \\[10pt] &= \frac{j\omega L_2}{j\omega L_2 + \frac{1}{j\omega C}} \times \frac{1}{j\omega C} \\[10pt] &= \frac{j\omega L_2}{j\omega L_2 \cdot j\omega C + \frac{1}{j\omega C} \cdot j\omega C} \\[10pt] &= \frac{j\omega L_2}{1 - \omega^2 L_2 C} \end{aligned} \]これでL₂とCの合成インピーダンス \(Z_{L_2C}\) が求まりました。
ええやん!これを使って回路全体のインピーダンス \(\dot{Z}\) を求めるで。RとL₁は直列やから足し算するだけやけど、どうなる?
はい!回路全体のインピーダンスは、R、L₁、そしてL₂とCの合成インピーダンスを直列に足し合わせます:
\[ \begin{aligned} \dot{Z} &= R + j\omega L_1 + \frac{j\omega L_2}{1 - \omega^2 L_2 C} \\[10pt] &= R + j\omega\left(L_1 + \frac{L_2}{1 - \omega^2 L_2 C}\right) \end{aligned} \]このように、実部(抵抗成分)とj倍の虚部(リアクタンス成分)に分けることができました。
ええで!直列共振するってことは、合成インピーダンスの虚部が0になるってことやな。せやから次の式が成り立つはずや:
\(L_1 + \frac{L_2}{1 - \omega_1^2 L_2 C} = 0\)
この式からω₁を求めてみてくれるか?
はい、解いてみます!直列共振条件から、インピーダンスの虚部が0になる式を変形していきます:
\[ \begin{aligned} L_1 + \frac{L_2}{1 - \omega_1^2 L_2 C} &= 0 \\[10pt] L_1 &= -\frac{L_2}{1 - \omega_1^2 L_2 C} \\[10pt] L_1 &= \frac{L_2}{\omega_1^2 L_2 C - 1} \\[10pt] L_1(\omega_1^2 L_2 C - 1) &= L_2 \\[10pt] \omega_1^2 L_1 L_2 C - L_1 &= L_2 \\[10pt] \omega_1^2 L_1 L_2 C &= L_1 + L_2 \\[10pt] \omega_1 &= \sqrt{\frac{L_1 + L_2}{L_1 L_2 C}} \end{aligned} \]これで直列共振角周波数ω₁の一般式が求まりました!
ナイス!じゃあ、実際の値を代入して計算してみよか。L₁ = 0.4×10⁻³ [H]、L₂ = 0.2×10⁻³ [H]、C = 8×10⁻⁶ [F]やで。
わかりました!これらの値を代入して直列共振角周波数ω₁を計算します:
\[ \begin{aligned} \omega_1 &= \sqrt{\frac{L_1 + L_2}{L_1 L_2 C}} \\[10pt] &= \sqrt{\frac{0.4 \times 10^{-3} + 0.2 \times 10^{-3}}{0.4 \times 10^{-3} \times 0.2 \times 10^{-3} \times 8 \times 10^{-6}}} \\[10pt] &= \sqrt{\frac{0.6 \times 10^{-3}}{0.4 \times 0.2 \times 8 \times 10^{-12}}} \\[10pt] &= \sqrt{\frac{0.6 \times 10^{-3}}{0.64 \times 10^{-12}}} \\[10pt] &= \sqrt{0.9375 \times 10^9} \\[10pt] &\approx 3.1 \times 10^4 \ \mathrm{[rad/s]} \end{aligned} \]したがって、直列共振角周波数ω₁は約3.1×10⁴ [rad/s]となります。
よっしゃ!次は並列共振角周波数ω₂を考えるで。並列共振とはどういう状態か知ってるか?
はい!並列共振とは、並列回路のアドミタンスが最小(インピーダンスが最大)になる状態です。この場合、L₂とCが並列になっている部分が共振して、その合成アドミタンスが0になるときに並列共振が起こります。
ええやん!じゃあL₂とCの合成アドミタンスを求めてみるで。アドミタンスは覚えてるか?インピーダンスの逆数やな。それぞれのアドミタンスを足し合わせればいいんや。
はい!アドミタンスはインピーダンスの逆数で、並列回路ではアドミタンスを足し合わせます。
コンデンサCのアドミタンス:\(Y_C = j\omega C\)
インダクタL₂のアドミタンス:\(Y_{L_2} = \frac{1}{j\omega L_2}\)
合成アドミタンスを計算します:
\[ \begin{aligned} Y_{合成} &= Y_C + Y_{L_2} \\[10pt] &= j\omega C + \frac{1}{j\omega L_2} \\[10pt] &= j\omega C - j\frac{1}{\omega L_2} \\[10pt] &= j\left(\omega C - \frac{1}{\omega L_2}\right) \end{aligned} \]並列共振条件では、この合成アドミタンスが0になります。
そうや!じゃあ、合成アドミタンスが0になる条件を考えよか。これでω₂が求められるで。
はい!合成アドミタンスが0になる条件を解きます:
\[ \begin{aligned} j\left(\omega C - \frac{1}{\omega L_2}\right) &= 0 \\[10pt] \omega C - \frac{1}{\omega L_2} &= 0 \\[10pt] \omega C &= \frac{1}{\omega L_2} \\[10pt] \omega^2 &= \frac{1}{L_2 C} \\[10pt] \omega_2 &= \frac{1}{\sqrt{L_2 C}} \end{aligned} \]これで並列共振角周波数の一般式が求まりました!
ええやん!じゃあ最後に数値を代入して、並列共振角周波数ω₂を求めてみよか。L₂ = 0.2×10⁻³ [H]、C = 8×10⁻⁶ [F]やったな。
はい!並列共振角周波数ω₂を計算します:
\[ \begin{aligned} \omega_2 &= \frac{1}{\sqrt{L_2 C}} \\[10pt] &= \frac{1}{\sqrt{0.2 \times 10^{-3} \times 8 \times 10^{-6}}} \\[10pt] &= \frac{1}{\sqrt{1.6 \times 10^{-9}}} \\[10pt] &= \frac{1}{4 \times 10^{-5}} \\[10pt] &= 2.5 \times 10^4 \ \mathrm{[rad/s]} \end{aligned} \]したがって、並列共振角周波数ω₂は2.5×10⁴ [rad/s]となります。
よくできたな!じゃあ、結論をまとめよか。直列共振角周波数ω₁と並列共振角周波数ω₂はそれぞれいくらやった?
はい!計算結果をまとめます:
・直列共振角周波数ω₁ = 3.1×10⁴ [rad/s]
・並列共振角周波数ω₂ = 2.5×10⁴ [rad/s]
よって、答えは選択肢の(5)となります。
ええやん!これでこの問題は完璧や!今回学んだのは「直列共振」と「並列共振」の違いやな。直列共振では合成インピーダンスの虚部が0になって、並列共振では合成アドミタンスが0になる。覚えておいてな!
はい、先生!とても勉強になりました!要点をまとめると:
1. 直列共振:インピーダンスの虚部が0になり、\(\omega_1 = \sqrt{\frac{L_1 + L_2}{L_1 L_2 C}}\)
2. 並列共振:合成アドミタンスが0になり、\(\omega_2 = \frac{1}{\sqrt{L_2 C}}\)
この式の違いとその導出過程をしっかり覚えておきます!
解説まとめ
①直列共振角周波数 \( \omega_{1} \)
\( C \) と \( L_{2} \) の合成インピーダンスは,
\[ \begin{aligned} \frac{ \mathrm{j} \omega L_{2} \cdot \frac{1}{\mathrm{j} \omega C} }{ \mathrm{j} \omega L_{2} + \frac{1}{\mathrm{j} \omega C} } &= \frac{ \mathrm{j} \omega L_{2} }{ \mathrm{j} \omega L_{2} + \frac{1}{\mathrm{j} \omega C} } \cdot \frac{1}{\mathrm{j} \omega C} \\ &= \frac{ \mathrm{j} \omega L_{2} }{ \mathrm{j} \omega L_{2} \cdot \mathrm{j} \omega C + \frac{1}{\mathrm{j} \omega C} \cdot \mathrm{j} \omega C } \\ &= \frac{ \mathrm{j} \omega L_{2} }{ 1 - \omega^2 L_{2} C } \end{aligned} \]
となるので,回路の合成インピーダンス \( \dot{Z} \) は,
\[ \begin{aligned} \dot{Z} &= R + \mathrm{j} \omega L_{1} + \frac{ \mathrm{j} \omega L_{2} }{ 1 - \omega^2 L_{2} C } \\ &= R + \mathrm{j} \omega \left( L_{1} + \frac{ L_{2} }{ 1 - \omega^2 L_{2} C } \right) \end{aligned} \]
と求められる。よって,直列共振するためには上式の虚数部が零となれば良いので,
\[ \begin{aligned} L_{1} + \frac{ L_{2} }{ 1 - \omega_{1}^2 L_{2} C } &= 0 \\ L_{1} &= \frac{ L_{2} }{ \omega_{1}^2 L_{2} C - 1 } \\ L_{1} ( \omega_{1}^2 L_{2} C - 1 ) &= L_{2} \\ \omega_{1}^2 L_{1} L_{2} C - L_{1} &= L_{2} \\ \omega_{1}^2 L_{1} L_{2} C &= L_{1} + L_{2} \\ \omega_{1} &= \sqrt{ \frac{ L_{1} + L_{2} }{ L_{1} L_{2} C } } \end{aligned} \]
となり,各値を代入すると,
\[ \begin{aligned} \omega_{1} &= \sqrt{ \frac{ 0.4 \times 10^{-3} + 0.2 \times 10^{-3} }{ 0.4 \times 10^{-3} \times 0.2 \times 10^{-3} \times 8 \times 10^{-6} } } \\ &\approx 3.1 \times 10^{4} \quad \mathrm{[rad/s]} \end{aligned} \]
②並列共振角周波数 \( \omega_{2} \)
並列共振するためには \( C \) と \( L_{2} \) の合成アドミタンスが零となればよい。\( C \) と \( L_{2} \) の合成アドミタンスは,
\[ \mathrm{j} \omega C + \frac{1}{\mathrm{j} \omega L_{2}} = \mathrm{j} \left( \omega C - \frac{1}{\omega L_{2}} \right) \]
と求められるので,並列共振周波数 \( \omega_{2} \) は,
\[ \begin{aligned} \omega_{2} &= \frac{1}{\sqrt{ L_{2} C }} \\ &= \frac{1}{\sqrt{ 0.2 \times 10^{-3} \times 8 \times 10^{-6} }} \\ &= 2.5 \times 10^{4} \quad \mathrm{[rad/s]} \end{aligned} \]